对勾函数和对号函数有什么特点对号函数和耐克函数是什么

对勾函数和对号函数有什么特点

说到对勾函数，它其实就是一种形似反比例函数的双曲函数，表达式长这样：f(x) = ax + b/x，且这里的a和b都得大于零。名字挺有意思，对勾函数也叫“双勾函数”、“勾函数”啥的，顾名思义，它的图像看起来就像对号或者勾子。

这类函数可不简单，当x大于0的时候，它还能有个最小值，这个最小值出现在x = √(b/a)的时候。这儿跟教科书里讲的可差不多哈，能用导数的朋友可以轻松证明。对勾函数的形状其实是两条抛物线分布在第一、第三象限，且不会和x轴或y轴相交，这点挺重要的。

对号函数一看名字跟对勾函数相近，但其实它不太一样。对号函数主要就是我们熟悉的绝对值函数f(x) = |x|，它的输出永远都是非负的，不管x本身正不正。说实话，这家伙在不同区间表现得分段线性——x≥0的时候就跟x一样，x小于0时，输出就是取它相反数，让人感觉特别直接和清晰。

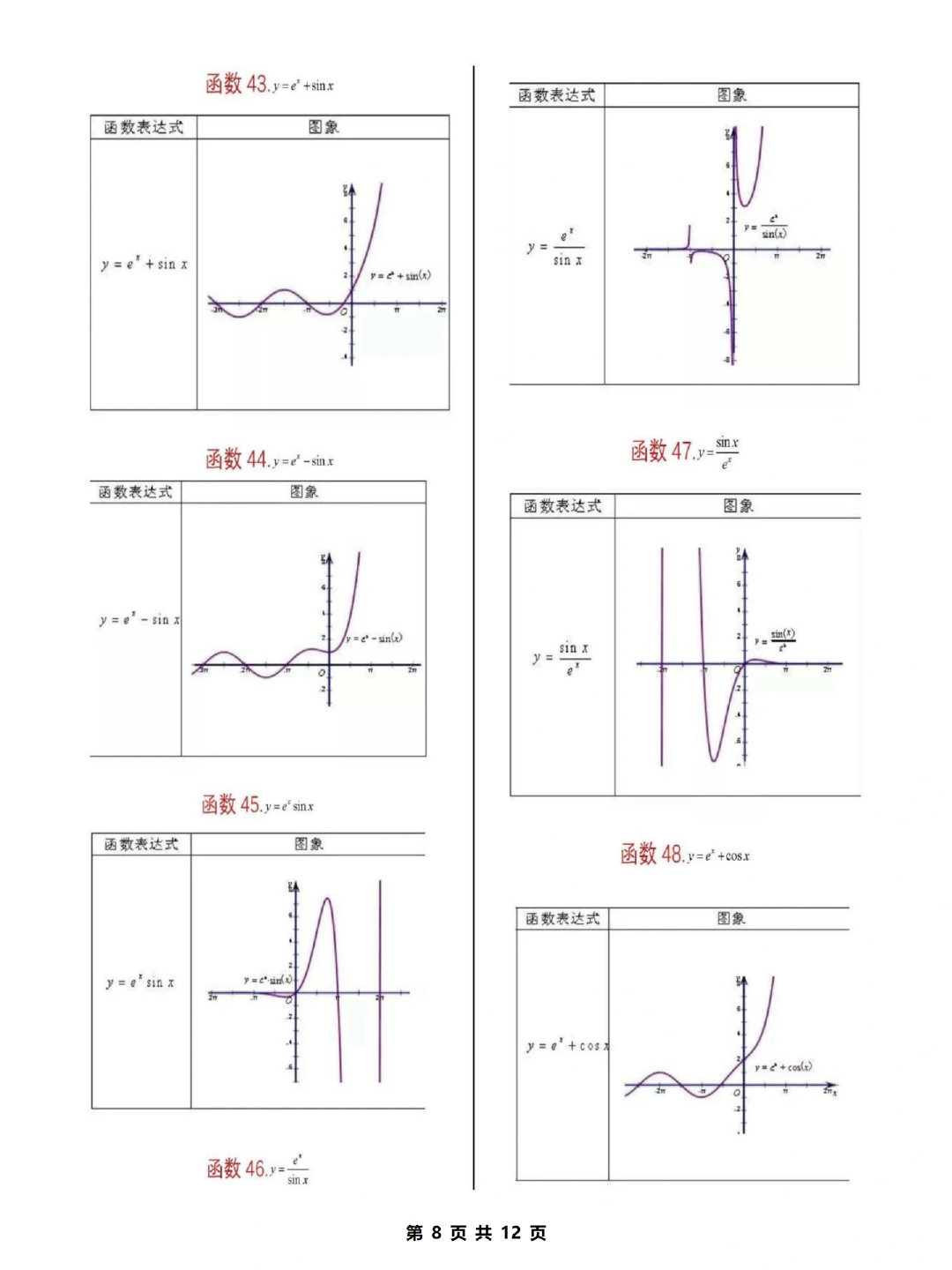
对勾函数和耐克函数的图像有哪些特别之处双勾函数符号变化会怎样

这里先说说双勾函数y = ax + b/x，a和b都不能是零，通常a、b各自有两种可能的符号组合，所以一共会有四种不同的图像形态。比如说，a>0且b>0的情况是最经典的，对勾函数的样子，图形很像耐克标志，它在第一象限像一个“勾”，两条渐近线分别是y = ax和x = 0，挺好辨认的。

耐克函数其实就是y = x + a/x，它的图像是双支双曲线，中心对称，看起来就像耐克的“钩”。这函数挺有意思的，它在负无穷到负根号a这一段是单调递增，接着负根号a到0单调递减，接着0到根号a区间又是单调递减，最后根号a到正无穷单调递增。听起来绕口，但看图就一目了然。不过超赞的是它的中心对称性，旋转180度和原图完全重合，超级酷。

另外，像y = ax + b/x这种函数，当ab>0时，大家有时候也叫它海鸥函数，因为图像像海鸥在海面翱翔的感觉；而ab<0则像两只海鸥斜插在海面。是不是很有画面感？这也帮咱们更容易记忆它们的图像变化。